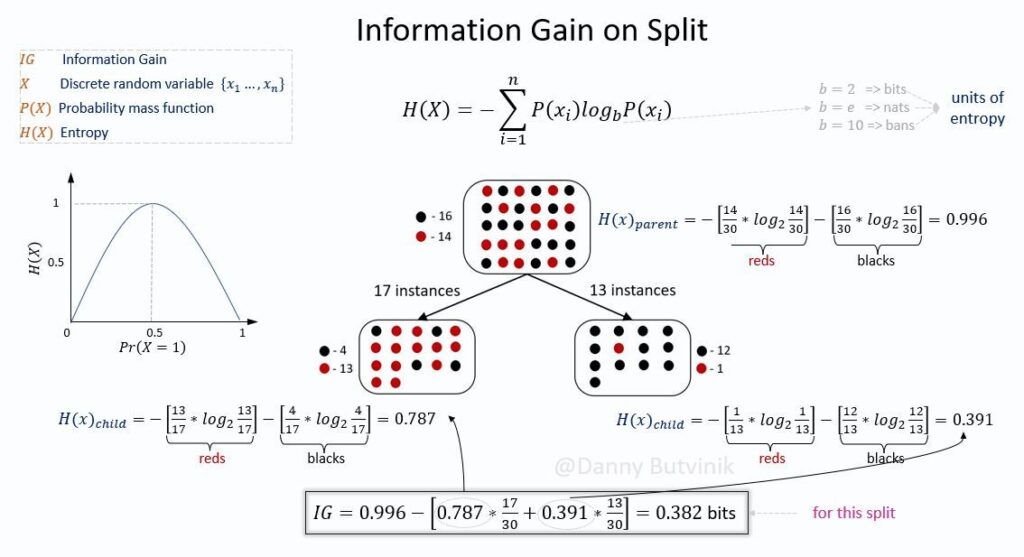
IG helps to determine the order of attributes in the nodes of a decision tree. The main node is referred to as the parent node, whereas sub-nodes are known as child nodes.
IG is the amount of information gained about a random variable from observing another random variable.
Entropy is the average rate at which information is a measure of the uncertainty associated with a random variable.
In Data Science and Machine Learning, IG is calculated for a split by subtracting the weighted entropies of each branch from the original entropy.
When training a Decision Tree using these metrics, the best split is chosen by maximizing information gain.
The variable that has the largest IG is selected to split the dataset. Generally, a larger gain indicates a smaller entropy or less surprise.
Entropy, as it relates to Machine Learning, is a measure of the randomness in the information being processed. The higher the entropy, the harder it is to draw conclusions from that information.
The lower the entropy in Machine Learning, the more accurate the prediction we can make. Due to the entropy measurement, we can decide which variables are the most efficient to split on, making a decision tree more effective and accurate.